こんにちは、タクトシステム制作チームです。
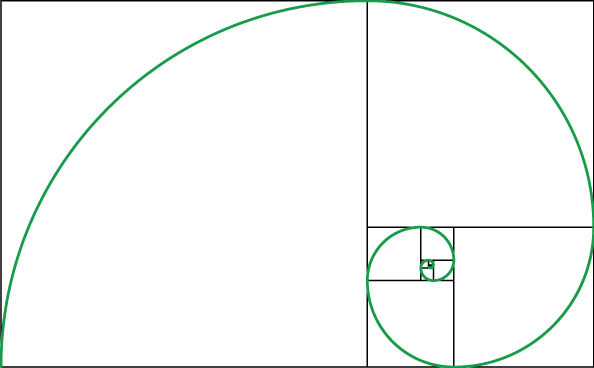
※螺旋
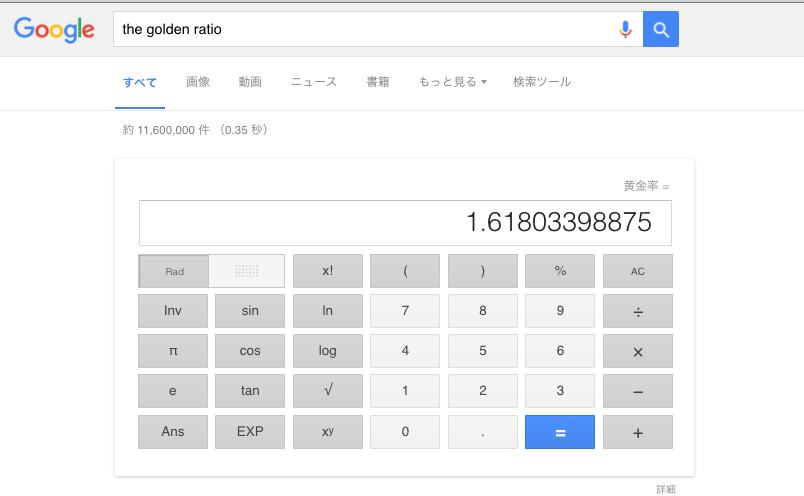
今回は黄金比についての話です。英語ではThe Golden Ratio。Googleで「The Golden Ratio」を検索すると電卓が出てきます。
黄金比とは
近似値は1:1.618、約5:8( Wikipediaより)
名刺の縦横サイズとか、美術や自然界、株式相場のテクニカル分析などさまざまな場面であらわれる不思議な数字です。この黄金比を計算するにはフィボナッチ数列を使用します。
フィボナッチ数列
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610...
最初の二項は1, 2で決めうちとし、以後どの項もその直前の二項の和となっています。つまり、3つ目の「3」は「1+2=3」で以降「2+3=5」「3+5=8」というわけです。さらに数列が進むにつれ直前の項とで割った数が約1.61803398875...に収斂します。この数字が黄金比です。
1. Excelで計算
上記の法則をExcelで計算することができます。
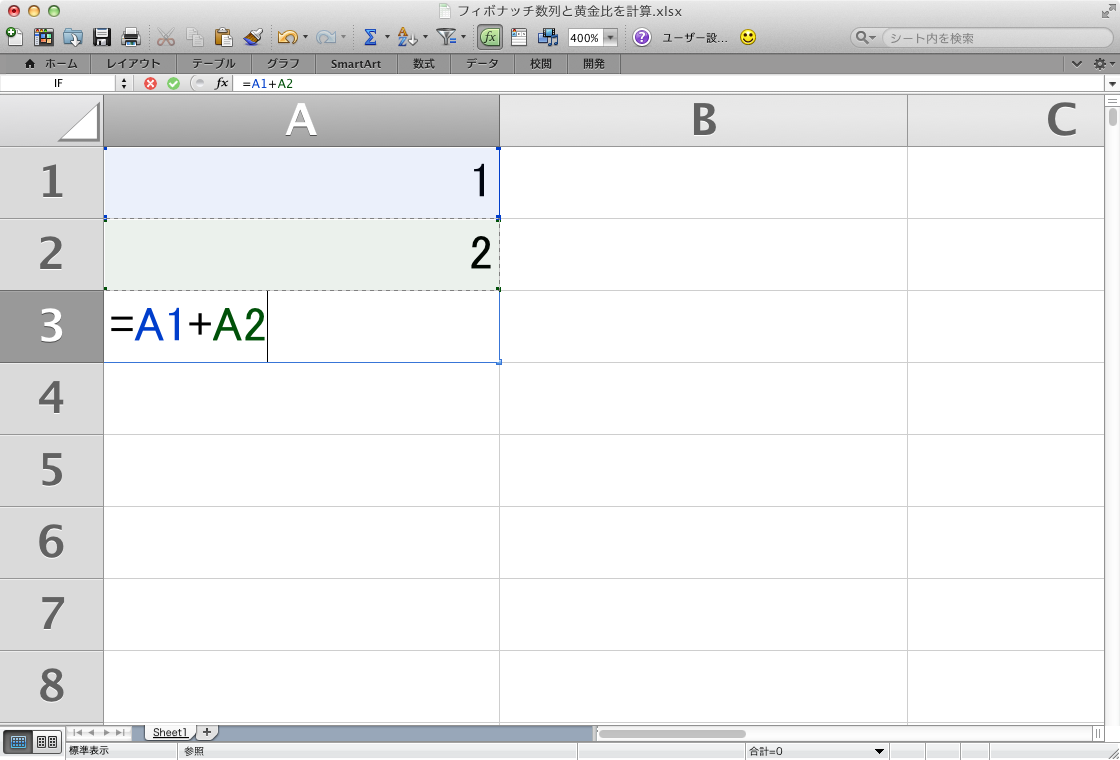
最初のセルA1に「1」を入力しセルA2は「2」を入力。
※セルA1に「1」を入力
※セルA2は「2」を入力
セルA3に計算式「=A1+A2」を入力しセル下までフィルすると自動的にフィボナッチ数列ができます!
※セルA3に計算式「=A1+A2」を入力
※セル下までフィルするとフィボナッチ数列ができる!
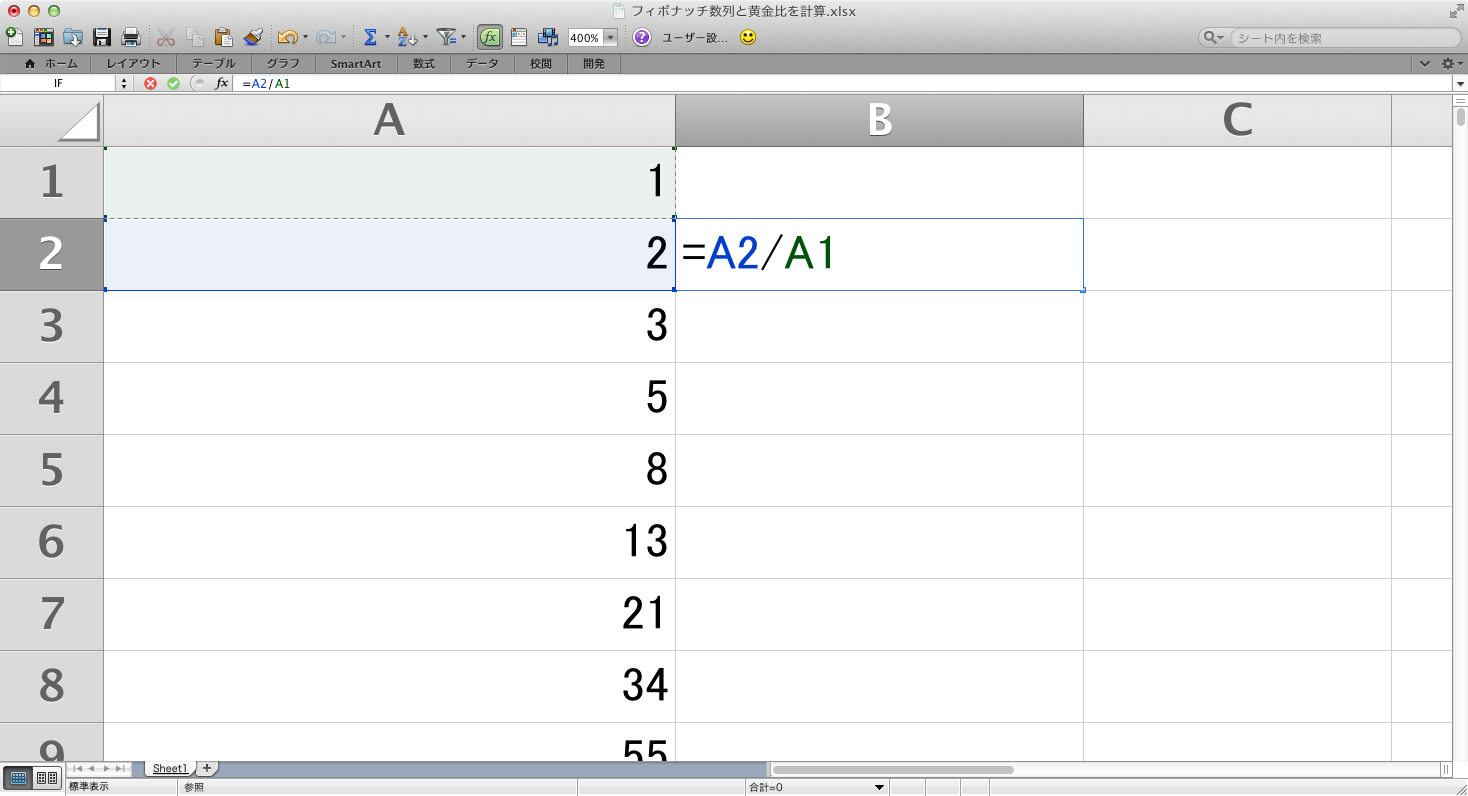
次はセルB2に計算式「=A2/A1」を入力。
※2÷1=2
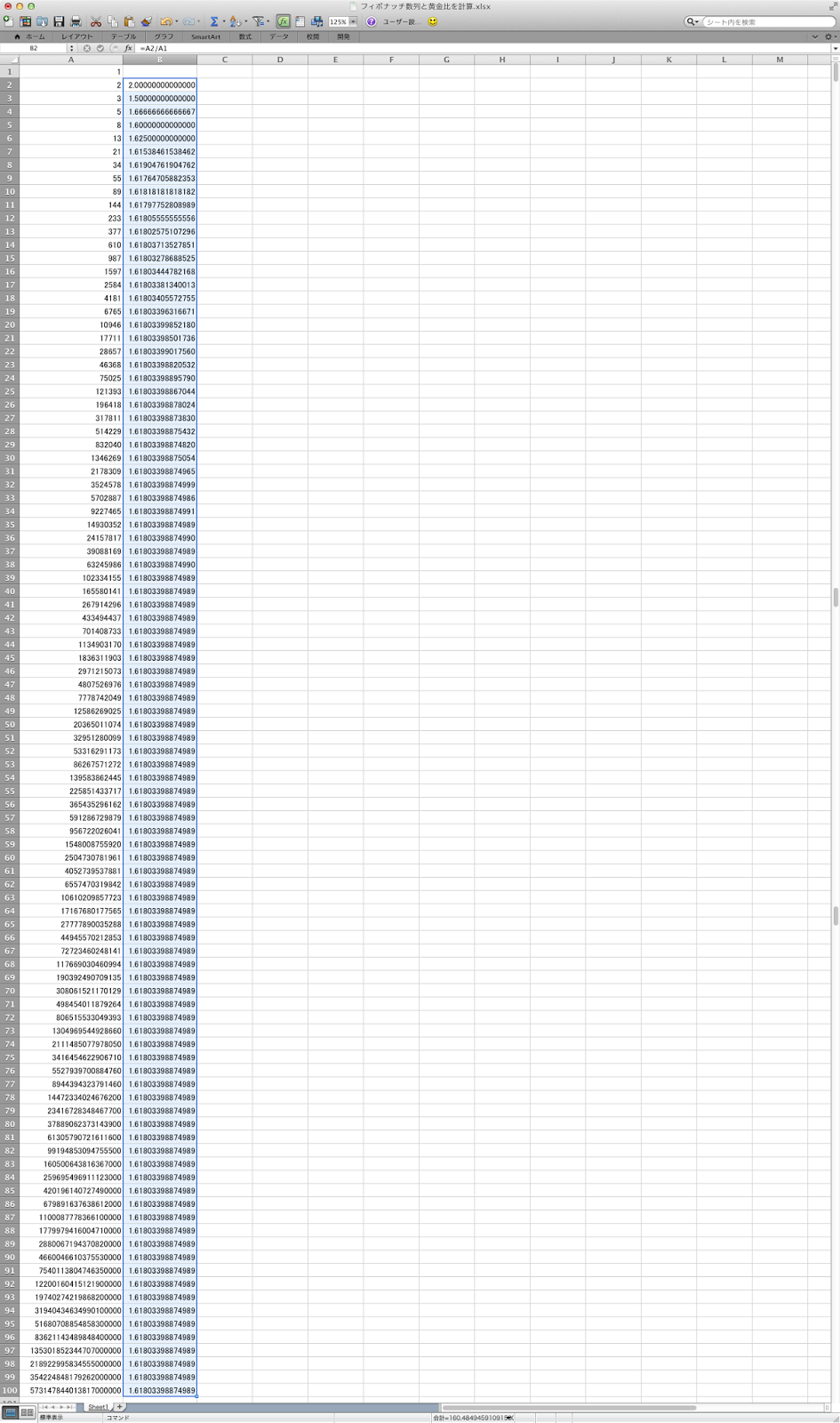
こちらもセル下までフィルすることで最初は「2」だった割り算の結果が「1.61803398874989」に収斂していきます。
※セル下までフィルすることで黄金比ができる!
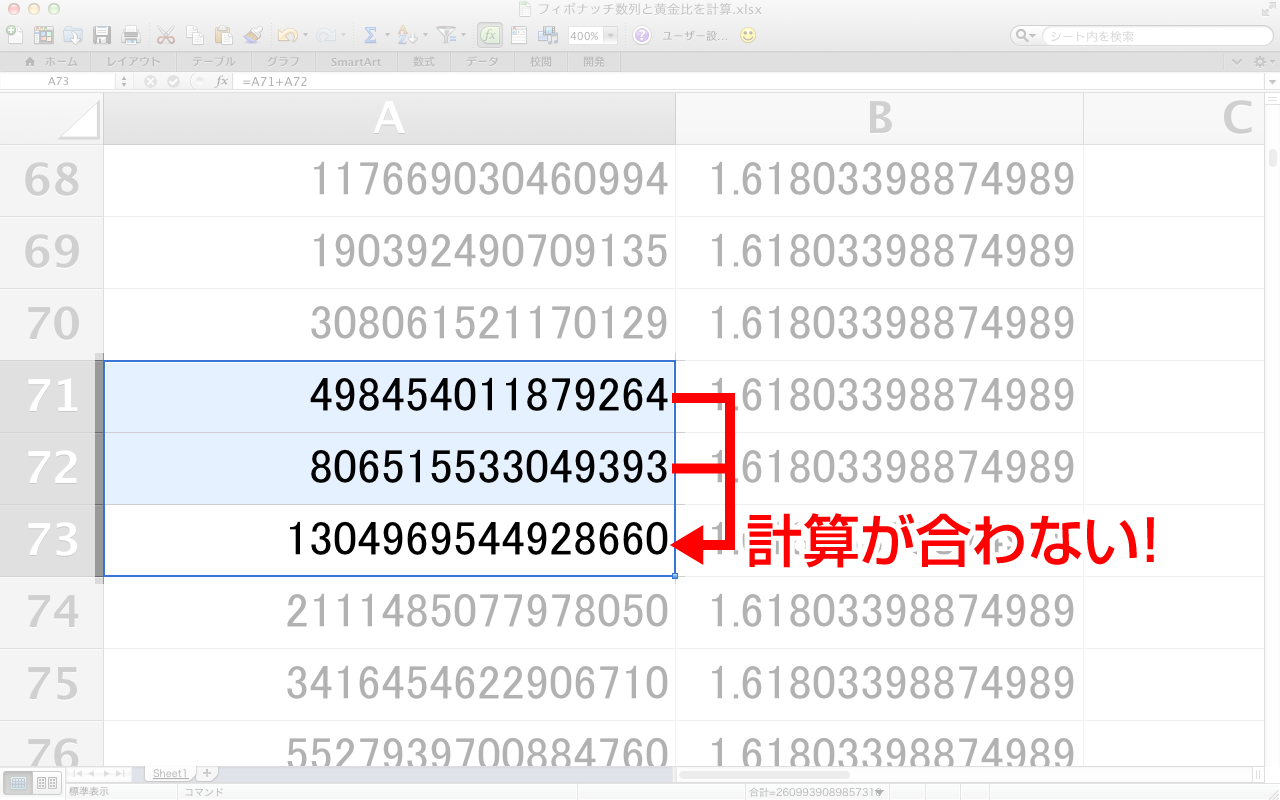
しかしとある箇所で計算がおかしいことに気がつきます。
「498454011879264+806515533049393=1304969544928657」なのに
「1304969544928660」と表示されています。
※1304969544928657のはずが
どうしてこうなるのでしょう? なんとこれはExcelの仕様で、セルに15桁を超える数字を入力すると、15桁目より下位のすべての桁がゼロに変更されるためだそうです(参考:Excel のセルに桁数の多い数字を入力すると最後の桁がゼロに変更される)。なんだそりゃ! しかし前項と割った数は「1.61803398874989」となっています。
2. AppleScriptで計算
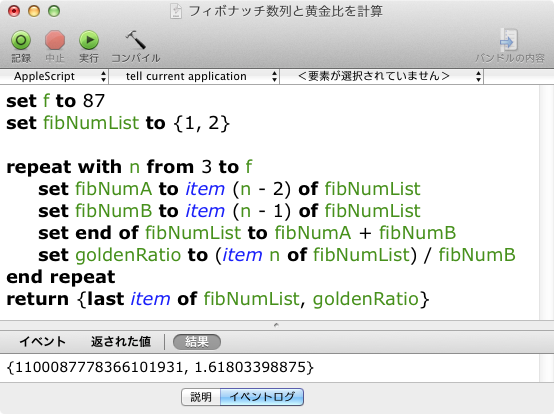
次にAppleScriptで計算してみました。
fibNumAが2つ前の項、fibNumBが1つ前の項で二項の和と割った数を求めています。こちらでは「1100087778366101931」まで正確に計算できましたが前項と割った数は「1.61803398875」でした。Excelに比べると小数点以下の数字が11位までしか表示されません。
ちなみに、上記のコードをAppleScript エディタで保存して再度開くと、「開けませんでした。」とアラートが…。どうもメモリが不足してしまうようでコンパイルできなくなってしまうようです。あらら。
大きな数を扱う場合はもっと精度の高いプログラムを使わないと険しいようです。